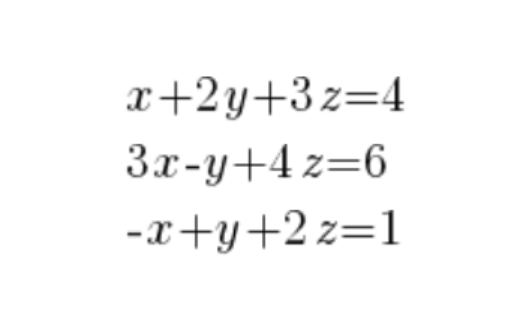Sistemas de ecuaciones y su resolución

Vamos a ver a continuación lo que son los sistemas de ecuaciones y su resolución y métodos.

Sea un sistema de ecuaciones de ejemplo:

~~~ x + 2y + 3z = 4
~~~ 3x - y + 4z = 6
~~~ - x + y + 2z = 1

Para poder resolver el sistema es importante tener en cuenta lo siguiente:

• La cantidad de ecuaciones m necesaria para resolver un sistema de ecuaciones donde tenemos n variables distintas, deberá ser al menos igual o mayor al número de variables, es decir, m~\geq~n.

Como podemos observar en nuestro ejemplo, tenemos 3 ecuaciones para 3 variables: x, y, z , lo cual garantizará que podamos resolver nuestro sistema. Luego analizaremos qué podría ocurrir si tenemos más ecuaciones que variables, lo cual también es algo a lo que hay que prestar atención, ya que podría dar lugar a una inconsistencia en el sistema o bien la interdependencia de alguna de esas ecuaciones entre sí. Pero eso, mejor veámoslo más delante. Ahora vamos a centrarnos en la resolución de un sistema de ecuaciones donde tenemos n = m, es decir, mismo número de variables que de ecuaciones. Empecemos pues.

Vamos a reducir el problema a un sistema de ecuaciones de 2 variables y 2 ecuaciones, ya que será más sencillo entender las operaciones que realicemos.

~~~ x + 2y = 4
~~~ x - y = 8

Bien, en este punto cabe destacar los distintos métodos por los que podemos optar en la resolución del sistema de ecuaciones:

• Método de sustitución.
• Método de reducción.
• Método de igualación.

Método de sustitución

Este método tratará de aislar las variables en las ecuaciones, de forma que una vez hecho, podamos sustituirlas en la ecuación restante que no haya intervenido en esa operación. Vamos con el ejemplo propuesto:

~~~ x + 2y = 4
~~~ x = 4 - 2y

Y una vez hecho esto, sustituiríamos en valor de esa variable en la ecuación o ecuaciones restante (nótese que estamos operando con 2 ecuaciones en el ejemplo, pero podríamos extenderlo a más ecuaciones).

Así que, procedemos:

~~~ x - y = 8
~~~ (4 - 2y) - y = 8
~~~ 4 - 3y = 8

Despejando:

~~~ y = \frac{8 - 4}{-3} = -\frac{4}{3}

Y por tanto:

~~~ x = 4 - 2y = 4 - 2~(-\frac{4}{3}) = 4 + \frac{8}{3} = \frac{20}{3}

Y como creemos que nuestra solución es correcta, únicamente nos quedará realizar la comprobación pertinente, que será escogiendo una de las ecuaciones y verificando la igualdad que manifiestan:

~~~ x - y = 8
~~~ \frac{20}{3}~-~( -\frac{4}{3} ) = 8
~~~ \frac{20}{3} + \frac{4}{3} = \frac{24}{3} = 8

Y en efecto, se verifica que nuestra resolución es correcta.

~~~ x = \frac{20}{3}
~~~ y = -\frac{4}{3}

Método de reducción

Este método por el contrario lo que va a buscar es la realización de alguna operación entre ecuaciones que reduzca el número de variables, de modo que se pueda despejar después de ello fácilmente. Pero, vayamos a ello y veámoslo con el ejemplo:

Dadas las ecuaciones:

~~~ x + 2y = 4
~~~ x - y = 8

Realizaremos una operación de resta de la primera menos la segunda, ya que el término x es igual en ambas ecuaciones. Si no fuese así, deberíamos forzarlo, multiplicando o dividiendo por el coeficiente adecuado. Después de esta operación, veremos en qué consiste esto, pero ahora vayamos a lo que hemos propuesto.

~~~ x + 2y - (x - y) = 4 - 8
~~~ 3y = -4
~~~ y = -\frac{4}{3}

y sustituyendo:

~~~ x = 4 - 2y = \frac{20}{3}

Y por tanto:

~~~ x = \frac{20}{3}
~~~ y = -\frac{4}{3}

Y como habíamos sugerido antes, vamos a ver qué haríamos si quisiéramos hacer esa reducción a través de la variable y:

~~~ x + 2y = 4
~~~ x - y = 8

Multiplicamos la segunda igualdad por 2:

~~~ x + 2y = 4
~~~ 2x - 2y = 16

Y al tener el término 2y y -2y en ambas ecuaciones, lo que hacemos en sumarlas, quedando así:

~~~ 3x = 20

Y despejando:

~~~ x = \frac{20}{3}
~~~ y = -\frac{4}{3}

Y vemos que llegamos al mismo punto.

Método de igualación

Y finalmente este método consistirá en la igualación de variables después de despejar ambas en sus respectivas

ecuaciones. Veamos:

Dadas:

~~~ x + 2y = 4
~~~ x - y = 8

Despejamos la x, por ejemplo:

~~~ x = 4 - 2y
~~~ x = 8 + y

E igualamos ambos términos:

~~~ 4 - 2y = 8 + y

Y despejando la y:

~~~ y = -\frac{4}{3}

Así que:

~~~ x = \frac{20}{3}
~~~ y = -\frac{4}{3}

Resumen

La resolución de sistemas de ecuaciones es relativamente sencilla, pero es muy importante dominarla en sus tres formas de resolución, ya que aparte de darnos más visión de cómo se puede operar, nos proporcionará una gran habilidad para elegir la que mejor se ajuste a las ecuaciones que tengamos que resolver.

Nota importante

En todo momento, los resultados se ofrecen en forma de fracciones, sin necesidad de recurrir a ningún cálculo para obtener un número con sus correspondientes decimales. Esto es absolutamente intencionado y necesario en el mundo de las matemáticas, donde el resultado se puede ofrecer de una forma conceptual, sin llegar a dar un resultado preciso, como a veces se da en disciplinas como la física. Y esto es sumamente importante tenerlo en cuenta. En el caso que nos ocupa, estamos hablando de fracciones en el campo de los número racionales, pero se vuelve si cabe más importante, cuando utilizamos números irracionales como pueden ser el número Pi, Phi o e, donde los resultados se deben mostrar en forma fracción sin llegar a ningún cálculo preciso. Obtenemos así formas más elegantes y conceptuales de los resultados, que de seguro agradarán a cualquiera que nos esté evaluando. Es decir:

Siempre será mejor y más elegante ofrecer un resultado tal que:

~~~ x = \frac{4}{3}
~~~ x = \frac{\pi}{2}

que no resultados de este tipo:

~~~ x = 1.3333...
~~~ x = 1.5707...

Y en esa línea, ofrezcan siempre resultados fraccionarios con números enteros en el numerador y el denominador, evitando por completo los decimales:

~~~ x = \frac{4}{3}~\pi^2~x^3

en vez de:

~~~ x = 13.15947~x^3

Y como digo, esto es un signo claro de elegancia matemática, y no invalida resultados con decimales, pero sí ensucia el resultado. Y en el caso de los números irracionales, cuyos decimales no se pueden modelizar, hará que nuestro resultado sea más incorrecto que el hecho de haber utilizado fracciones.

¡¡Felices mates!!