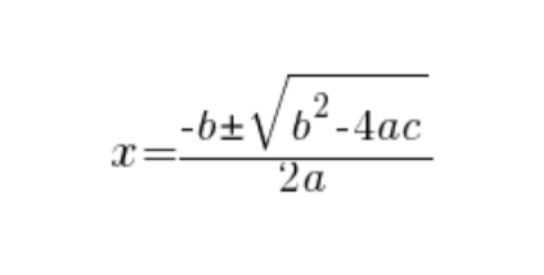La resolución de ecuaciones de segundo grado es una de las actividades más usuales en el mundo de las matemáticas por ser una operación muy frecuente. Aquí voy a abordar su fórmula, pero sobre todo, cómo se obtiene.
~~~ a~x^2 + b~x + c = 0Vamos a despejar las variables y veremos al final la famosa ecuación con la que se obtienen los valores de x. Para ello vamos a recordar cual es resultado del cuadrado de un polinomio de primer grado:
~~~ (x~+~a)^2 = x^2 + 2~a~x + a^2Esto es importante porque vamos a tratar de convertir esa ecuación de 2º grado en un cuadrado de una ecuación de primer grado:
Dividimos por a, y obtenemos:
~~~ x^2 + \frac{b}{a}~x + \frac{c}{a} = 0Multiplicamos y dividimos por 2 el segundo término de la ecuación:
~~~ x^2 + 2~\frac{b}{2~a}~x + \frac{c}{a} = 0Sumamos y restamos por el término que hará que podamos convertir los sumandos en una ecuación de primer grado elevado al cuadrado:
~~~ x^2 + 2~\frac{b}{2~a} x + ({\frac{b}{2~a}})^2 - ({\frac{b}{2~a}})^2 + \frac{c}{a} = 0Convertimos los tres primeros sumandos en un cuadrado de un polinomio de primer grado:
~~~ (x + \frac{b}{2~a})^2 - \frac{b^2}{4~a^2} + \frac{c}{a} = 0Despejamos la x, y tenemos que:
\newline ~~~ (x + \frac{b}{2~a})^2 = \frac{b^2}{4~a^2} - \frac{c}{a} = \frac{b^2}{4~a^2} - \frac{4~a~c}{4~a^2} = \frac{b^2~-~4~a~c}{4~a^2} \newline ~~~ x + \frac{b}{2~a} = \pm~\sqrt{ \frac{{b^2}~-~{4~a~c}}{4~a^2} } \newline ~~~ x = -~\frac{b}{2~a}~\pm~\sqrt{ \frac{{b^2}~-~{4~a~c}}{4~a^2} } \newline ~~~ x = -~\frac{b}{2~a}~\pm~\frac{1}{2~a}~\sqrt{ {{b^2}~-~{4~a~c}} } \newline ~~~ x = \frac{-~b~\pm~\sqrt{ {{b^2}~-~{4~a~c}} } }{2~a}Convertimos los tres primeros sumandos en un cuadrado de un polinomio de primer grado:
Pues, como podéis comprobar, de una forma sencilla y sabiendo operar con los cuadrados de los polinomios de primer grado, previamente preparados, llegamos a la famosa ecuación que todos conocemos en la resolución de ecuaciones de segundo grado.
~~~ \boxed{x = \frac{-~b~\pm~\sqrt{ {{b^2}~-~{4~a~c}} } }{2~a} }Es muy importante notar que el resultado obtenido son dos soluciones, ya que estamos ante una ecuación de segundo grado:
~~~ x_1 = \frac{-~b~+~\sqrt{ {{b^2}~-~{4~a~c}} } }{2~a} \newline \newline ~~~ x_2 = \frac{-~b~-~\sqrt{ {{b^2}~-~{4~a~c}} } }{2~a}Así es que, como habéis podido comprobar, es sencillo, pero a la vez requiere cierta operativa llegar a la fórmula a aplicar, pero quizás lo más interesante de todo es el proceso, y haber podido saber hacer todos esos pasos que nos llevan a la fórmula final.
¡Felices mates!!