La trigonometría

Esta disciplina de las matemáticas es fundamental para entender múltiples cuestiones matemáticas que tengan que ver con el espacio y la posición en el mismo, y en la concepción circular del espacio y de las coordenadas.

Veamos la representación de una circunferencia y conceptualicemos todo:

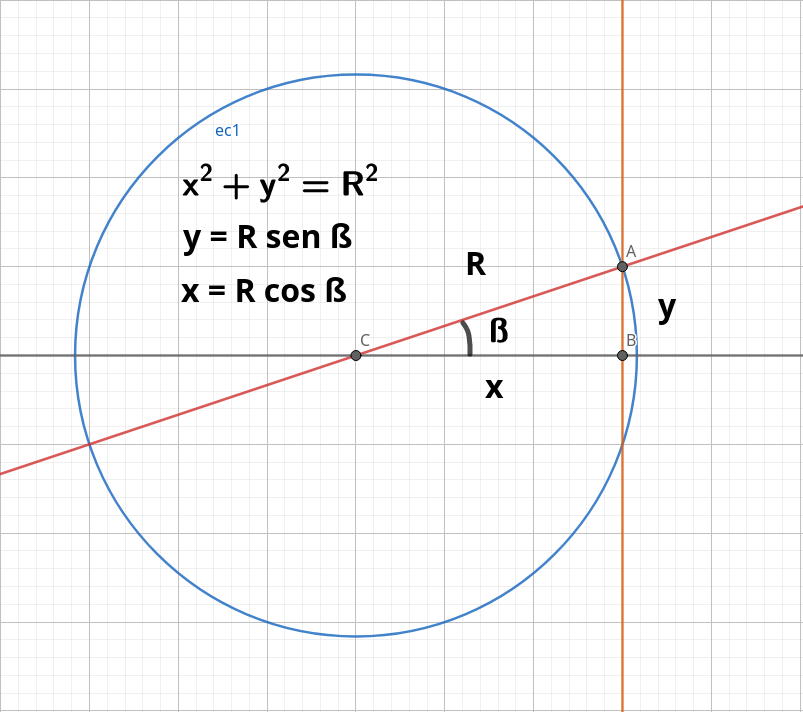
Es decir, que dada una circunferencia, cualquier punto que define su trayectoria viene determinado por unas coordenadas x e y, que cumplen:

~~~ x = R~cos~\beta
~~~ y = R~sin~\beta

Por lo que:

~~~ cos~\beta = x / R
~~~ sin~\beta = y / R

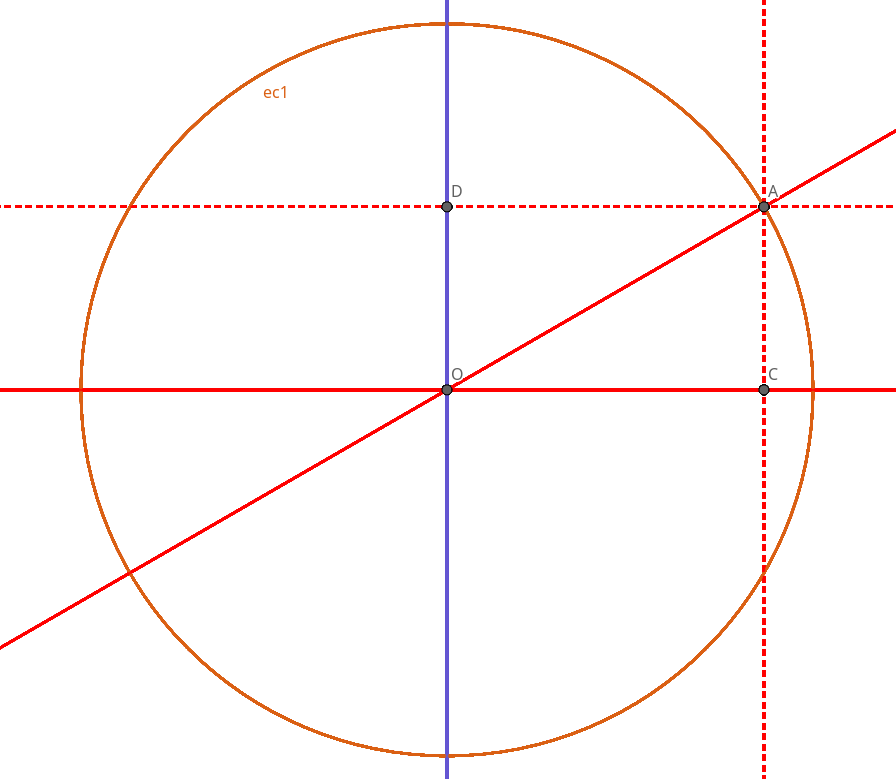
Es decir, que tanto el coseno como el seno no son más que las razones entre la proyección sobre el eje de las abscisas u de las ordenadas del punto que intersecta con una hipotética circunferencia y el radio de esta circunferencia. Así es que si nos dan un ángulo tan sólo, podemos dibujar dos rectas que formen ese ángulo, de forma que una de las rectas descanse sobre un hipotético eje de abscisas, y una circunferencia de radio cualquiera, y construir un triángulo rectángulo con tres puntos:

• El punto de intersección de las dos rectas, centro de nuestra circunferencia.
• El punto de intersección de una de las rectas con la circunferencia creada.
• El punto de proyección del anterior punto de intersección sobre la recta que está situada sobre el eje de abscisas, o también el punto de proyección del anterior punto de intersección sobre la recta que representaría un hipotético eje de ordenadas.

Reproduzcamos el proceso:

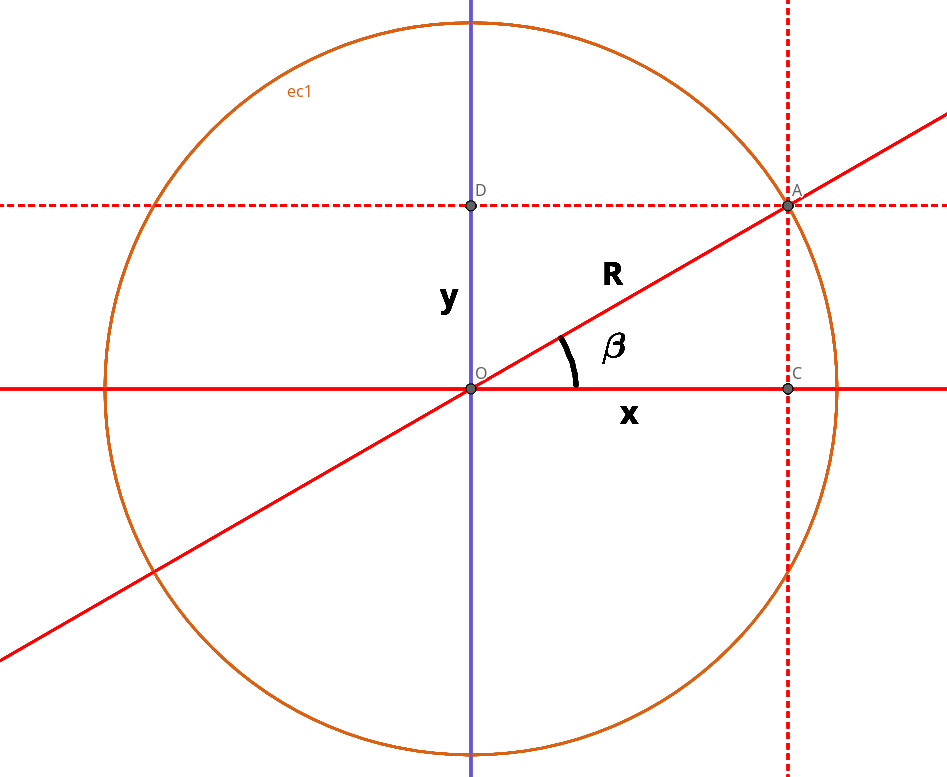
Aquí surgen dos conceptos fundamentales, como son el seno y el coseno de un ángulo, que puestos en un sistemas de coordenadas, como el que se describe en el gráfico, determinan el número de 0 a 1 que multiplica al radio de la hipotética circunferencia en nuestro sistema de coordenadas establecido con el que se obtendrá, o bien la x (el caso del coseno) o bien la y (el caso del seno).

Otra de las razones importantes en trigonometría sería la tangente, y la cotangente (inversa de la tangente), que sería:

~~~ tg~\beta = {sen~\beta} / {cos~\beta}
~~~ cotg~\beta = {cos~\beta} / {sen~\beta}
~~~ cotg~\beta = {1 / {tg~\beta}}

A continuación daré los valores de los cosenos y senos para los ángulos más frecuentes:

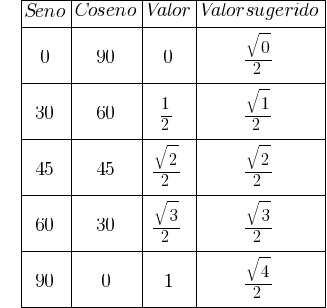
La trigonometría nace del propio teorema de Pitágoras, de aplicación en los triángulos rectángulos, cuyo enunciado dice que: «el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos».

~~~ h^2 = a^2 + b^2

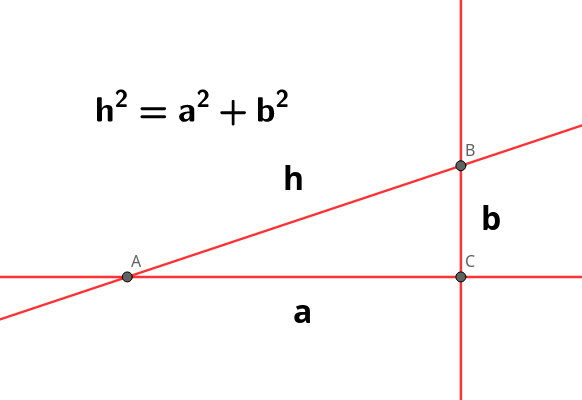
Como podemos esta es la base de la propia trigonometría, ya que nuestra hipotenusa es el radio de la circunferencia de la que hemos empezado hablando para ilustrar las razones trigonométricas. Y así, refrescando lo que teníamos inicialmente, podemos ver el por qué, y la razón de donde surge, y desde aquí trabajaremos en algunas otras fórmulas trigonométricas bien conocidas. Aplicando a la circunferencia que teníamos inicialmente:

~~~ R^2 = x^2 + y^2

De modo que, si revisamos las ecuaciones propuestas en base al seno y al coseno, tenemos:

~~~ x = R~cos~\beta
~~~ y = R~sen~\beta

y despejando en nuestra ecuación pitagoriana:

~~~ R^2 = (R~cos~\beta)^2 + (R~sen~\beta)^2
~~~ R^2 = R^2~cos^2~\beta + R^2~sen^2~\beta
~~~ R^2 = R^2~(cos^2~\beta + sen^2~\beta)

Y finalmente:

~~~ 1 = cos^2~\beta + sen^2~\beta

Con lo que ya tenemos otra ecuación que nos acompañará permanentemente en nuestro periplo a través de la trigonometría y su aplicación. Por supuesto, de esta misma tenemos otras formas:

~~~ cos^2~\beta = 1~-~sen^2~\beta

Como se puede observar, toda la trigonometría descansa sobre la base del teorema de Pitágoras, y está íntimamente relacionada con las representaciones circulares y con el número Pi. El número Pi es una pieza clave y fundamental de la trigonometría en la medición de los ángulos. Empecemos de momento midiendo la longitud de una circunferencia. Sea pues:

~~~ L = 2~\pi~R

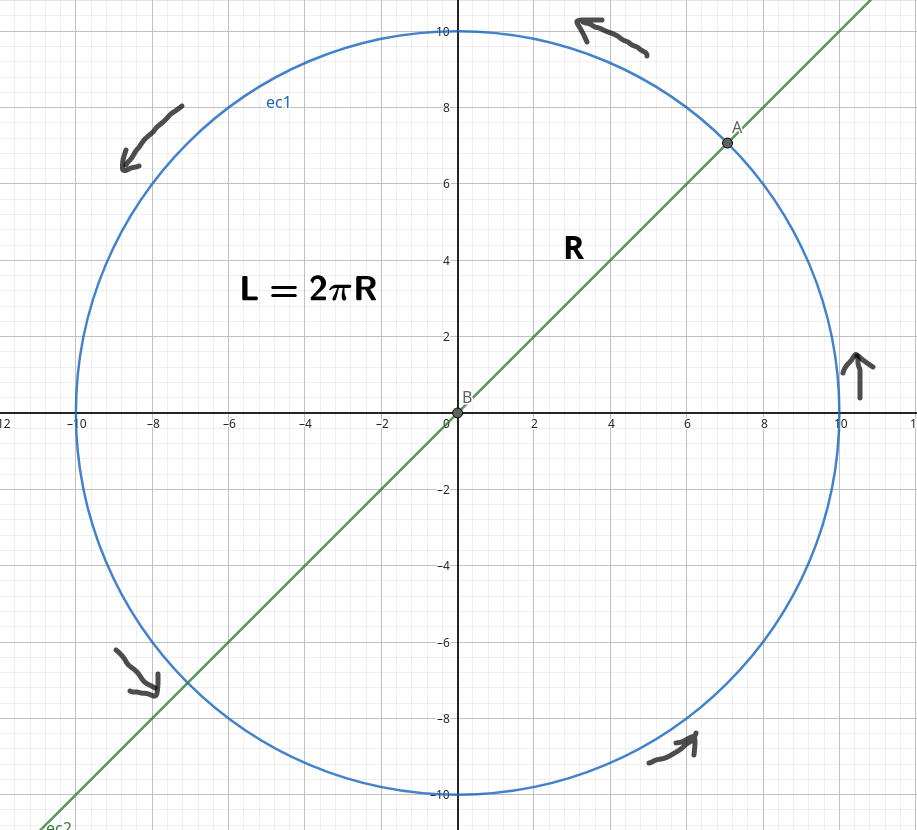
La longitud de una circunferencia equivale a 2 veces Pi por el radio de la circunferencia. Pero si queremos hallar la longitud de un tramo de circunferencia:

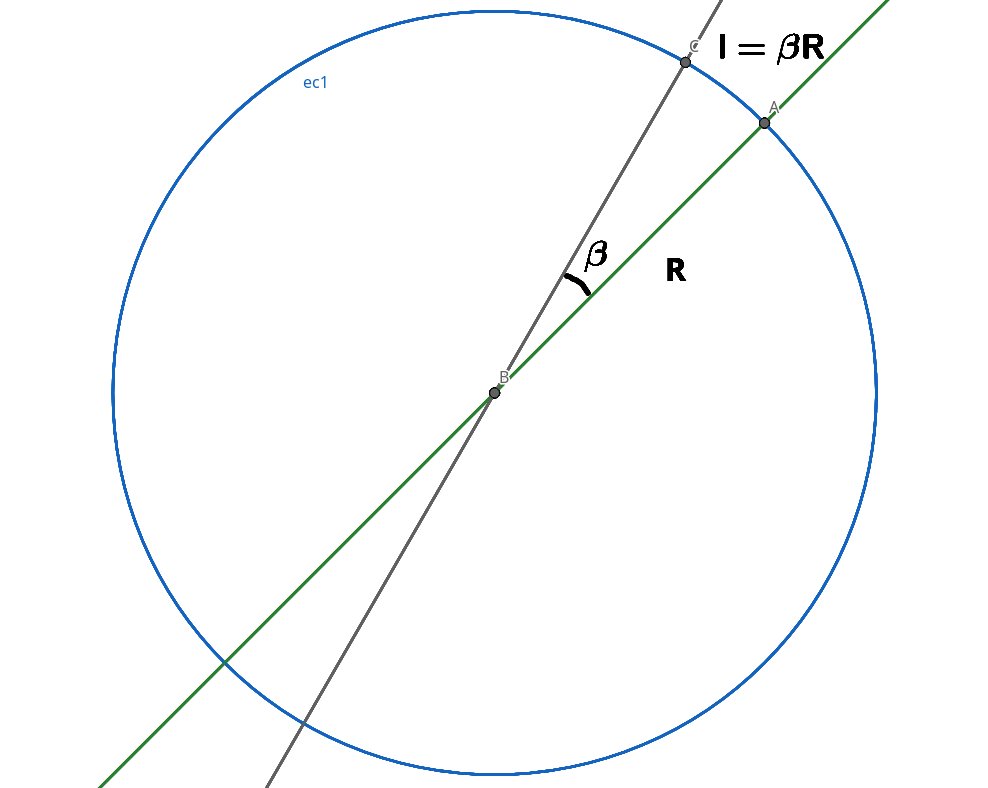
De esto se desprende que:

Del gráfico vemos que \beta es el ángulo por el que multiplica el radio para hallar una revolución de una circunferencia, y como este toma el valor de 2 \pi, sabemos que una circunferencia toma valores de ángulo entre 0 y 2\pi en una circunferencia completa. Es importante notar que ese valor del ángulo está medido en radianes.

A continuación podemos ver una representación de las equivalencias entre ángulos medidos en grados y en radianes:

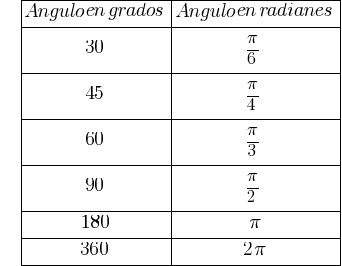
De ahora en adelante, será crucial el manejo de \pi como unidad fundamental de los ángulos. A continuación podemos observar una sencilla ecuación de transformación de grados a radianes:

~~~ rad = {{2~\pi} / 360}~x , donde x es el ángulo en grados y rad es el ángulo en radianes que se obtiene

Así que, de ahora en adelante será muy frecuente el encontrarnos con formas mixtas de exponernos los ángulos, y debemos ser capaces de entenderlas:

~~~ sen~90^o = sen~{\pi/2}
~~~ cos~180^o = cos~\pi

Y finalmente, hemos abordado los senos y los cosenos, pero lo hemos hecho tomando ángulos menores de 90 grados, pero no hemos abordado su valor en el conjunto de la circunferencia. No varía mucho, pero sí lo hace en cuanto a los signos que toman los valores. Es importante que tengamos en cuenta que los valores de los cosenos y de los senos no son más que el valor de la proyección del punto en la circunferencia en los ejes de abscisas (cosenos) y de ordenadas (senos), de forma que la razón entre la longitud proyectada y el propio radio de la circunferencia nos da el valor del seno (eje de ordenadas o y) o del coseno (eje de abscisas o x).