La derivada de una función

La derivada de una función es un concepto muy relevante en el mundo de las matemáticas y que define la variación infinitesimal de una función en un punto.

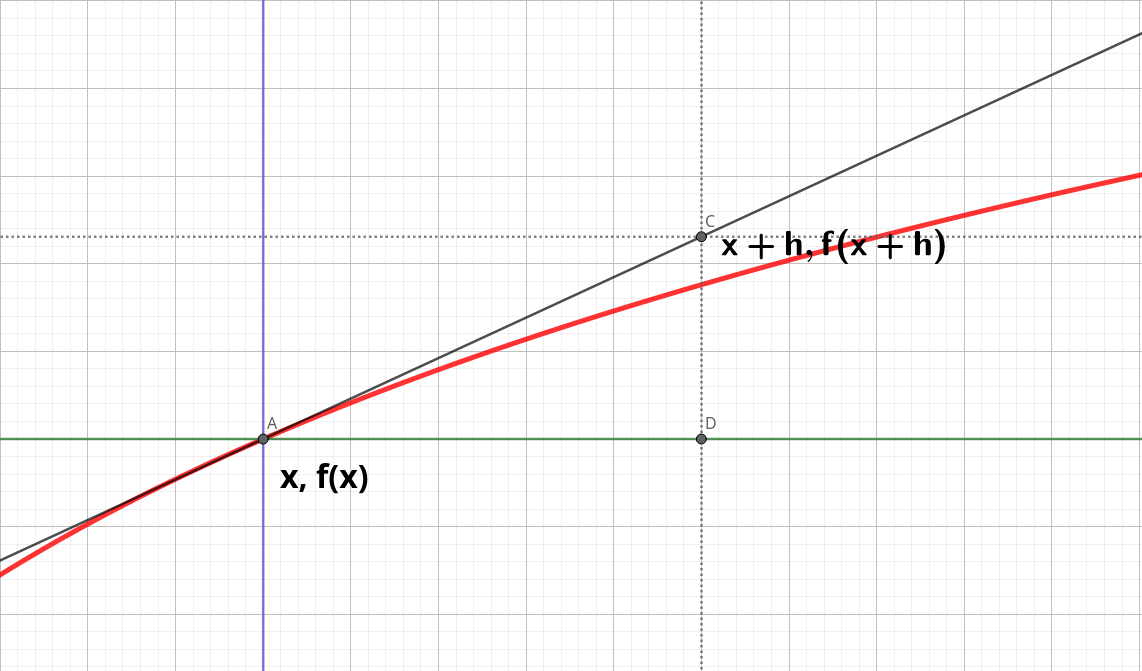
Vamos inicialmente a ver conceptualmente qué es una derivada. Para ello, sea la gráfica que vemos a continuación, con dos puntos muy próximos entre sí:

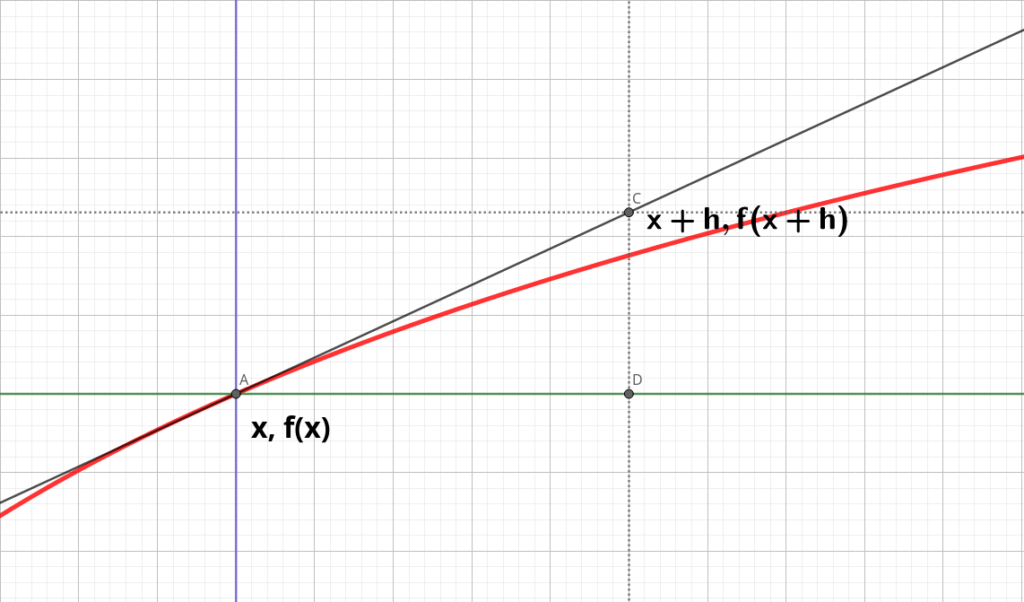
En el gráfico podemos observar la curva de una función en color rojo, y un punto A ( x, f(x) ) en esa curva cuya tangente a la curva genera una recta que nos ayudará a entender el concepto de derivada. También vemos otro punto C ( x+h, f(x+h) ), siendo h una cantidad dada que hace aumentar x. Como podemos observar, la recta tangente en un punto de la curva, se va alejando progresivamente según aumentamos h, pero si lo que hacemos es disminuir h, lo que ocurre es que el valor de ese punto de la tangente cada vez se aproxima más al propio valor en la curva.

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{(x+h)-x} = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}

Es decir, que la razón entre el incremento de la ordenada ( f(x+h)-f(x) ) y el incremento de la abscisa ( h ) cuando este incremento h tiende a ser 0, es en realidad el valor de la tangente del ángulo en ese punto de la función en cuestión, y será la derivada de esa función en ese punto, algo que se utilizará muy recurrentemente en el análisis de las funciones para hallar los puntos máximos y mínimos, es decir, aquellos puntos cuya tangente tiene como valor 0 por ser rectas paralelas al eje de abscisas y por tanto con ángulo 0, cuya tangente es 0.

Derivadas conocidas

~~~ y = f(x) = f(g(x)) ~~~ \Rightarrow ~~~ y\prime = f\prime(x) = \frac{df}{dg}~·~\frac{dg}{dx}
~~~ y = f(x) = w(x) + t(x) ~~~ \Rightarrow ~~~ y\prime = f\prime(x) = w\prime(x) + t\prime(x) = w\prime + t\prime
~~~ y = f(x) = w(x)~t(x) ~~~ \Rightarrow ~~~ y\prime = f\prime(x) = w\prime(x)~t(x) + w(x)~t\prime(x) = w\prime~t + w~t\prime
~~~ y = f(x) = \frac{w(x)}{t(x)} ~~~ \Rightarrow ~~~ y\prime = f\prime(x) = \frac{w\prime(x)~t(x) - w(x)~t\prime(x)}{t^2(x)} = \frac{w\prime~t - w~t\prime}{t^2}
~~~ y = f(x) = c_n x^n + c_{n-1} x^{n-1} + ... + c_1 x + c_0 ~~~ \Rightarrow ~~~ y\prime = f\prime(x) = c_n n x^{n-1} + c_{n-1} (n-1) x^{n-2} + ... + c_2 2 x + c_1
~~~ y = f(x) = ln~x ~~~ \Rightarrow ~~~ y\prime = f\prime(x) = \frac{1}{x}
~~~ y = f(x) = log_a~x ~~~ \Rightarrow ~~~ y\prime = f\prime(x) = \frac{1}{x~ln~a}
~~~ y = f(x) = sen~x ~~~ \Rightarrow ~~~ y\prime = f\prime(x) = cos~x
~~~ y = f(x) = cos~x ~~~ \Rightarrow ~~~ y\prime = f\prime(x) = -sen~x
~~~ y = f(x) = tg~x ~~~ \Rightarrow ~~~ y\prime = f\prime(x) = \frac{1}{cos^2~x}

~~~

Vayamos pues, una vez conocidas las derivadas más frecuentes, a su demostración, para ser conscientes de cómo se llega a la conclusión de cual es la función derivada de una establecida.

Demostración para una función de funciones (regla de la cadena)

Veamos:

Suponiendo las funciones g(x) y f(g(x)) derivables para todo x:

~~~ y = f(x) = f(g(x))
~~~ y\prime = f\prime(x) = \frac{df}{dx} = \frac{df}{dg}~·~\frac{dg}{dx}

Se comprueba así:

~~~ f\prime(x) = lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} = lim_{\Delta x \rightarrow 0} \frac{\Delta f}{\Delta g}~·~\frac{\Delta g}{\Delta x} = lim_{\Delta g \rightarrow 0} \frac{\Delta f}{\Delta g}~·~lim_{\Delta x \rightarrow 0} \frac{\Delta g}{\Delta x} = \frac{df}{dg}~·~\frac{dg}{dx}
~~~ f\prime(x) = \frac{df}{dx} = \frac{df}{dg}~·~\frac{dg}{dx}
~~~ \boxed{\frac{df}{dx} = \frac{df}{dg}~·~\frac{dg}{dx}}

~~~

Demostración para una suma de funciones

Veamos este caso:

~~~ y = f(x) = w(x) + t(x)
~~~ y\prime = f\prime(x) = w\prime(x) + t\prime(x)

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{w(x+h) + t(x+h) - ( w(x) + t(x) )}{(x+h)-x}

Si reorganizamos términos:

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{w(x+h) - w(x)}{h} + lim_{h \rightarrow 0} \frac{t(x+h) - t(x)}{h} = w\prime(x) + t\prime(x)
~~~ \boxed{ f\prime(x) = w\prime(x) + t\prime(x) }

~~~

Demostración para un producto de funciones

Veamos el caso del producto de dos funciones:

~~~ y = f(x) = w(x)~t(x)
~~~ y\prime = f\prime(x) = w\prime(x)~t(x) + w(x)~t\prime(x)

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{w(x+h)~t(x+h) - w(x)~t(x)}{(x+h)-x} = lim_{h \rightarrow 0} \frac{w(x+h)~t(x+h) - w(x)~t(x) + w(x)~t(x+h) - w(x)~t(x+h)}{(x+h)-x}

Ahora vamos a sumar y restar w(x)~t(x+h):

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{w(x+h)~t(x+h) - w(x)~t(x) + w(x)~t(x+h) - w(x)~t(x+h)}{(x+h)-x}

Ahora reorganicemos los términos:

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{t(x+h)~(w(x+h) - w(x)) + w(x)~( t(x+h) - t(x) ) }{h} = lim_{h \rightarrow 0} \frac{t(x+h)~(w(x+h) - w(x))}{h} + lim_{h \rightarrow 0} \frac{ w(x)~( t(x+h) - t(x) ) }{h}
~~~ f\prime(x) = lim_{h \rightarrow 0} t(x+h)~lim_{h \rightarrow 0} \frac{w(x+h) - w(x)}{h} + lim_{h \rightarrow 0} w(x)~lim_{h \rightarrow 0} \frac{ t(x+h) - t(x) }{h} = t(x)~w\prime(x) + w(x)~t\prime(x)
~~~ \boxed{ f\prime(x) = t(x)~w\prime(x) + w(x)~t\prime(x) }
~~~

Demostración para una división de funciones

Resolvamos el caso de una división de funciones, que será el caso de la derivada de un producto y de la derivada de un polinomio. Veamos pues:

~~~ y = f(x) = \frac{w(x)}{t(x)} = w(x)~t(x)^{-1}
~~~ y\prime = f\prime(x) = w\prime(x)~t(x) + w(x)~t\prime(x)

Sabiendo que:

~~~ f(x) = w(x)~t(x) \Rightarrow f\prime(x) = w\prime(x)~t(x) + w(x)~t\prime(x)
~~~ f(x) = \frac{1}{t(x)} = t(x)^{-1} \Rightarrow f\prime(x) = (-1)~t(x)^{-1-1} = - t(x)^{-2} = -\frac{1}{t(x)^2}~t\prime(x)

Tenemos que:

~~~ f\prime(x) = (w(x)~t(x)^{-1})\prime = w\prime(x)~t(x)^{-1} + w(x)~(t(x)^{-1})\prime = w\prime(x)~t(x)^{-1} + w(x)~(-\frac{1}{t(x)^2}) = \frac{w\prime(x)~t(x) - w(x)~t\prime(x)}{t(x)^2}
~~~ \boxed{f\prime(x) = \frac{w\prime(x)~t(x) - w(x)~t\prime(x)}{t(x)^2}}

~~~

Demostración para una función polinómica

Vamos a ilustrar esto que acabamos de exponer con un ejemplo de una función de x polinómica de la que sabremos su derivada fácilmente, y veamos qué ocurre:

Sea:

~~~ y = f(x) = c_n~x^n + c_{n-1}~x^{n-1} + ... + c_1~x + c_0

Su derivada es:

~~~ y\prime = f\prime(x) = c_n~n~x^{n-1} + c_{n-1}~(n-1)~x^{n-2} + ... + c_2~2~x + c_1

Y ahora apliquemos lo que hemos aprendido:

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{f(x+h)~-~f(x)}{(x+h)-x} = lim_{h \rightarrow 0} \frac{f(x+h)~-~f(x)}{h}
~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{(c_n~(x+h)^n~+~c_{n-1}~(x+h)^{n-1}~+~c_{n-2}~(x+h)^{n-2}~+~...~+~c_2~(x+h)^2~+~c_1~(x+h)~+~c_0)~-~(c_n~x^n~+~c_{n-1}~x^{n-1}~+~c_{n-2}~x^{n-2}~+~...~+~c_2~x^2~+~c_1~x~+~c_0)}{h}
~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{(~c_n~(x+h)^n-~c_n~x^n)~+~(c_{n-1}~(x+h)^{n-1}~-~c_{n-1}~x^{n-1}~)~+~(~c_{n-2}~(x+h)^{n-2}~-~c_{n-2}~x^{n-2}~)~+~...~+~(~c_2~(x+h)^2-c_2~x^2~)~+~(~c_1~(x+h)-~c_1~x~)~+~(~c_0-~c_0)~)}{h}

Sabiendo:

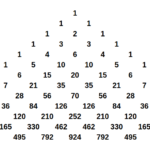
~~~ (x+h)^n = \binom{n}{0}~x^n~h^0 + \binom{n}{1}~x^{n-1}~h^1 + \binom{n}{2}~x^{n-2}~h^2 + ... + \binom{n}{n-1}~x^{n-(n-1)}~h^{n-1} + \binom{n}{n}~x^{n-n}~h^n
~~~ (x+h)^n = \binom{n}{0}~x^n + \binom{n}{1}~x^{n-1}~h + \binom{n}{2}~x^{n-2}~h^2 + ... + \binom{n}{n-1}~x~h^{n-1} + \binom{n}{n}~h^n
~~~ (x+h)^n = \sum_{i=0}^{n}\binom{n}{i}~x^{n-i}~h^i = \binom{n}{0}~x^n + h~(\sum_{i=1}^{n}\binom{n}{i}~x^{n-i}~h^{i-1}) = \binom{n}{0}~x^n + h~(~\binom{n}{1}~x^{n-1} + \sum_{i=2}^{n}\binom{n}{i}~x^{n-i}~h^{i-1}~)
~~~ (x+h)^n = x^n + h~(~\binom{n}{1}~x^{n-1} + \sum_{i=2}^{n}\binom{n}{i}~x^{n-i}~h^{i-1}~)
~~~ c_n~(x+h)^n = c_n~x^n + h~c_n~(~\binom{n}{1}~x^{n-1} + \sum_{i=2}^{n}\binom{n}{i}~x^{n-i}~h^{i-1}~)
~~~ c_n~(x+h)^n - c_n~x^n = h~c_n~(~\binom{n}{1}~x^{n-1} + \sum_{i=2}^{n}\binom{n}{i}~x^{n-i}~h^{i-1}~)

Con ello tenemos:

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{(~h~(~c_n~\binom{n}{1}~x^{n-1}~+~c_n~\sum_{i=2}^{n}\binom{n}{i}~x^{n-i}~h^{i-1}~)~)~+~(~h~(~c_{n-1}~\binom{n-1}{1}~x^{(n-1)-1}~+~c_{n-1}~\sum_{i=2}^{n-1}\binom{n-1}{i}~x^{(n-1)-i}~h^{i-1}~)~)~+~...~+~h~(~c_2~2~x~+c_2~h~)~+~h~c_1~)}{h}
~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{h~(~(~c_n~\binom{n}{1}~x^{n-1}~+~c_n~\sum_{i=2}^{n}\binom{n}{i}~x^{n-i}~h^{i-1}~)~+~(~c_{n-1}~\binom{n-1}{1}~x^{(n-1)-1}~+~c_{n-1}~\sum_{i=2}^{n-1}\binom{n-1}{i}~x^{(n-1)-i}~h^{i-1}~)~+~...~+~(~c_2~2~x~+c_2~h~)~+~c_1~)~)}{h}
~~~ f\prime(x) = lim_{h \rightarrow 0} (~c_n~\binom{n}{1}~x^{n-1}~+~c_n~\sum_{i=2}^{n}\binom{n}{i}~x^{n-i}~h^{i-1}~)~+~(~c_{n-1}~\binom{n-1}{1}~x^{(n-1)-1}~+~c_{n-1}~\sum_{i=2}^{n-1}\binom{n-1}{i}~x^{(n-1)-i}~h^{i-1}~)~+~...~+~(~c_2~2~x~+c_2~h~)~+~c_1~)
~~~ f\prime(x) = c_n~\binom{n}{1}~x^{n-1}~+~c_{n-1}~\binom{n-1}{1}~x^{(n-1)-1}~+~...~+~c_2~2~x~+~c_1
~~~ \boxed{f\prime(x) = c_n~n~x^{n-1}~+~c_{n-1}~(n-1)~x^{(n-1)-1}~+~...~+~c_2~2~x~+~c_1}
~~~ f\prime(x) = \sum_{i=1}^n c_i~i~x^{i-1}

Veamos ahora el caso particular:

Sea:

~~~ y = f(x) = 4 x^3 + 5 x + 3

Su derivada es:

~~~ y\prime = 12 x^2 + 5

Y ahora apliquemos lo que hemos aprendido:

~~~ f(x+h) = 4 (x+h)^3 + 5 (x+h) + 3 = 4 (x^3 + 3 x^2 h + 3 x h^2 + h^3) + 5 (x+h) + 3 = 4 x^3 + 12 x^2 h + 12 x h^2 + 4 h^3 + 5 x + 5 h + 3
~~~ f(x) = 4 x^3 + 5 x + 3

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{(x+h)-x} = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} = lim_{h \rightarrow 0} \frac{4 x^3 + 12 x^2 h + 12 x h^2 + 4 h^3 + 5 x + 5 h + 3 - 4 x^3 - 5 x - 3}{h} = lim_{h \rightarrow 0} \frac{12 x^2 h + 12 x h^2 + 4 h^3 + 5 h}{h} = lim_{h \rightarrow 0} \frac{h ( 12 x^2 + 12 x h + 4 h^2 + 5)}{h} = lim_{h \rightarrow 0} 12 x^2 + 12 x h + 4 h^2 + 5

Y aplicando el límite cuando h tiende a 0:

~~~ y\prime = f\prime(x) = 12 x^2 + 5

Y en efecto, ha quedado demostrado la derivada de la función y su valor tal como lo conocemos.

En realidad, de forma genérica para una función polinómica se tiene que, siendo la función:

~~~ f(x) = c_n x^n + c_{n-1} x^{n-1} + ... + c_1 x + c_0

Su derivada será:

~~~ \boxed{ f\prime(x) = c_n n x^{n-1} + c_{n-1} (n-1) x^{n-2} + ... + c_2 2 x + c_1 }
~~~

Demostración para una potencia

Vamos a ver el caso de una potencia. Pero básicamente, podemos decir que es el caso particular de una función polinómica reducida a la expresión de una potencia.

Si tenemos:

~~~ y = f(x) = a^n

Su derivada será:

~~~ y = f\prime(x) = n~a^{n-1}

Y como hemos dicho antes, no tendríamos más que revisar el caso de una función polinómica y eliminar los términos que no nos hagan falta y los coeficientes que sobren, y tendremos que:

~~~ \boxed{y = f\prime(x) = n~a^{n-1}} ~~~

Demostración para el logarítmo

Veamos ahora otro ejemplo distinto. Sea una función logarítmica en base n:

Sea:

~~~ y = f(x) = log_n (x) = log_n (x)

Su derivada es:

~~~ y\prime = f\prime(x) = \frac{1}{ln (a)~x}

Así que:

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{(x+h)-x} = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} = lim_{h \rightarrow 0} \frac{log_a (x+h) - log_a (x)}{h} = lim_{h \rightarrow 0} log_a (\frac{x+h}{x})^\frac{1}{h} = lim_{h \rightarrow 0} log_a (1 + \frac{h}{x})^\frac{1}{h} = log_a lim_{h \rightarrow 0} (1 + \frac{h}{x})^\frac{1}{h}

Ahora hacemos:

~~~ h = n~x

Y tenemos:

~~~ f\prime(x) = log_a lim_{n \rightarrow 0} (1 + n)^{\frac{1}{n}~\frac{1}{x}} = \frac{1}{x}~log_a~lim_{n \rightarrow 0} (1 + n)^{\frac{1}{n}} = \frac{1}{x}~log_a~e

Y sabiendo que:

~~~ log_a x = \frac{log_b x}{log_b a}

Tendremos que:

~~~ f\prime(x) = \frac{1}{x}~log_a~e = \frac{1}{x}~\frac{log_e~e}{log_e~a} = \frac{1}{x}~\frac{1}{ln~a}
~~~ \boxed{f\prime(x) = \frac{1}{x~ln~a}}

~~~

Demostración para el logarítmo neperiano

Veamos ahora otro ejemplo distinto. Sea una función logarítmica en base e, y veamos su derivada de la misma forma que hemos hecho antes:

Sea:

~~~ y = f(x) = ln (x) = log_e (x)

Su derivada es:

~~~ y\prime = \frac{1}{x}

Aplicando:

~~~ f(x+h) = ln (x+h)
~~~ f(x) = ln (x)

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{(x+h)-x} = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} = lim_{h \rightarrow 0} \frac{ln (x+h) - ln (x)}{h} = lim_{h \rightarrow 0} ln (\frac{x+h}{x})^\frac{1}{h} = lim_{h \rightarrow 0} ln (1 + \frac{h}{x})^\frac{1}{h}

Si ahora hacemos:

~~~ n = \frac{h}{x} \rightarrow h = n x

Con ello:

~~~ n \rightarrow 0 ~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{(x+h)-x} = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} = lim_{h \rightarrow 0} \frac{ln (x+h) - ln (x)}{h} = lim_{h \rightarrow 0} ln (\frac{x+h}{x})^\frac{1}{h} = lim_{h \rightarrow 0} ln (1 + \frac{h}{x})^\frac{1}{h}

Sustituimos h por n · x:

~~~ f\prime(x) = lim_{n \rightarrow 0} ln (1 + \frac{n x}{x})^\frac{1}{(n x)} = lim_{n \rightarrow 0} ln (1 + n)^{ {\frac{1}{n}} {\frac{1}{x}} } = lim_{n \rightarrow 0} \frac{1}{x} ln (1 + n)^{ {\frac{1}{n}} } = \frac{1}{x} lim_{n \rightarrow 0} ln (1 + n)^{ {\frac{1}{n}} } = \frac{1}{x} ln ( lim_{n \rightarrow 0} (1 + n)^{ {\frac{1}{n}} } )

Y sabiendo que:

~~~ lim_{n \rightarrow 0} (1 + n)^{ {\frac{1}{n}} } = e

Tenemos finalmente que:

~~~ f\prime(x) = \frac{1}{x} ln (e) = \frac{1}{x}
~~~ \boxed{ f\prime(x) = \frac{1}{x} }

~~~

Demostración para el seno

Veamos ahora el caso del seno:

Sea:

~~~ y = f(x) = sen (x)

Su derivada es:

~~~ y\prime = cos (x)

Ahora desarrollemos la derivada:

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{(x+h)-x} = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} = lim_{h \rightarrow 0} \frac{sen (x+h) - sen (x)}{h}

Sabiendo que:

~~~ sen(a+b) = sen(a)~cos(b) + sen(b)~cos(a)

Tenemos:

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{sen(x)~cos(h) + sen(h)~cos(x) - sen(x)}{h} = lim_{h \rightarrow 0} \frac{sen(x)~(cos(h) - 1) + sen(h)~cos(x)}{h} = lim_{h \rightarrow 0} \frac{sen(x)~(cos(h) - 1)}{h} + lim_{h \rightarrow 0} \frac{sen(h)~cos(x)}{h} = sen(x)~lim_{h \rightarrow 0} \frac{cos(h) - 1}{h} + cos(x)~lim_{h \rightarrow 0} \frac{sen(h)}{h}

Y aquí tenemos dos límites que resolver:

~~~ lim_{h \rightarrow 0} \frac{cos(h) - 1}{h} = 0
~~~ lim_{h \rightarrow 0} \frac{sen(h)}{h} = 1

Con lo que finalmente:

~~~ \boxed{ f\prime(x) = cos(x) } ~~~

Demostración para el coseno

Veamos ahora el caso del coseno:

Sea:

~~~ y = f(x) = cos (x)

Su derivada es:

~~~ y\prime = -sen (x)

Ahora desarrollemos la derivada:

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{(x+h)-x} = lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h} = lim_{h \rightarrow 0} \frac{cos (x+h) - cos (x)}{h}

Sabiendo que:

~~~ cos(a+b) = cos(a)~cos(b) - sen(b)~sen(a)

Tenemos:

~~~ f\prime(x) = lim_{h \rightarrow 0} \frac{cos(x)~cos(h) - sen(x)~sen(h) - cos(x)}{h} = lim_{h \rightarrow 0} \frac{cos(x)~(cos(h) - 1) + sen(x)~sen(h))}{h} = cos (x)~lim_{h \rightarrow 0} \frac{cos(h) - 1}{h} - sen(x)~lim_{h \rightarrow 0} \frac{sen(h)}{h}

Y aquí tenemos dos límites que resolver:

~~~ lim_{h \rightarrow 0} \frac{cos(h) - 1}{h} = 0
~~~ lim_{h \rightarrow 0} \frac{sen(h)}{h} = 1

Con lo que finalmente:

~~~ \boxed{ f\prime(x) = -sen(x) } ~~~

Demostración para la tangente

Veamos ahora el caso de la tangente:

Sea:

~~~ y = f(x) = tg (x) = \frac{sen(x)}{cos(x)} = sen( x)~cos(x)^{-1}

Su derivada es:

~~~ y\prime = f\prime(x) = \frac{1}{cos^2 x}

Ahora desarrollemos la derivada:

~~~ f\prime(x) = \frac{(sen(x))\prime~cos(x) - sen(x)~(cos(x))\prime}{cos^2(x)} = \frac{cos(x)~cos(x) - sen(x)~(-sen(x))}{cos^2(x)} = \frac{cos^2(x) + sen^2(x)}{cos^2(x)} = \frac{1}{cos^2(x)}
~~~ \boxed{f\prime(x) = \frac{1}{cos^2 x}}

~~~

Concepto de derivabilidad y continuidad en la derivación

Cuando estamos manejando el concepto de derivada de una función, cabe destacar que es importante que dicha función sea contínua en dicho punto en su definición. En los anteriores casos hemos asumido que las funciones eran derivables en un dominio completo de los números reales en un intervalo abierto desde -\infty a +\infty, y los resultados de las demostraciones son genéricas para dichos intervalos.

Y en cuanto a la continuidad de las funciones será importante tener en cuenta que la continuidad de las funciones a la hora de derivar es necesaria pero no suficiente, ya que existirán casos que a pesar de existir una continuidad, sin embargo presentan problemas en su derivabilidad, léase el caso de una función como f(x) = |x| .