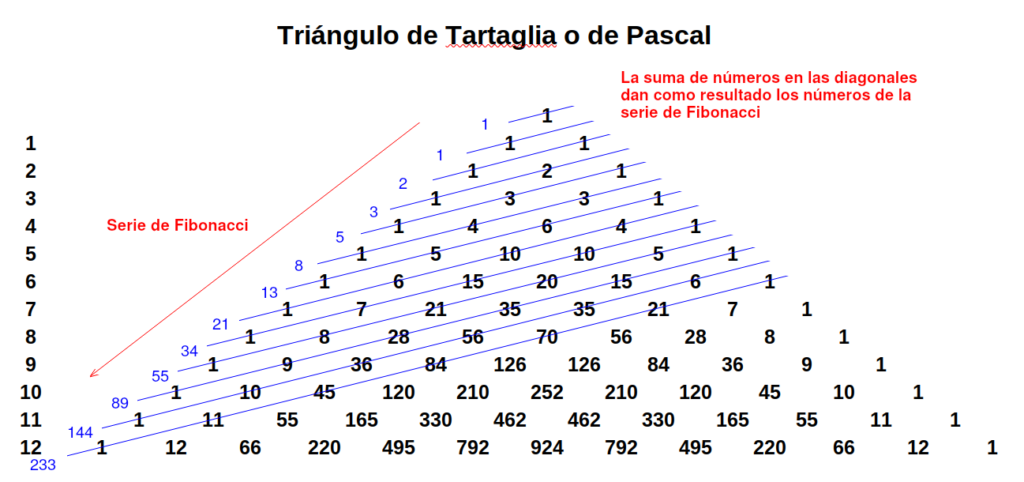
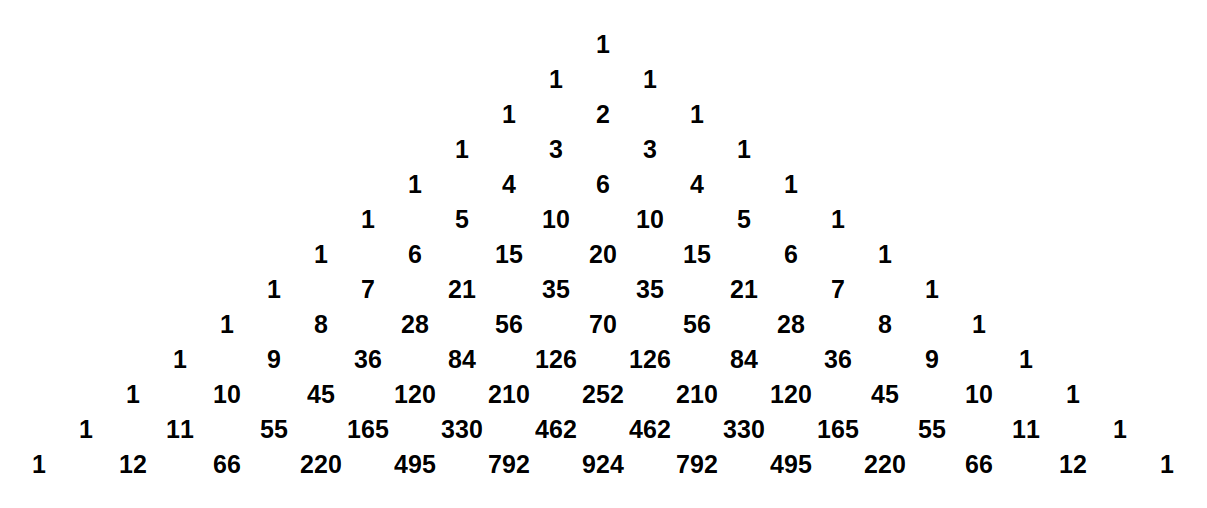
El triángulo de Tartaglia o de Pascal es harto conocido en el mundo de las matemáticas ya desde tiempos pretéritos. Su forma es la siguiente:

Este triángulo es enormemente útil para establecer los coeficientes en ecuaciones binomiales elevados a la n-ésima potencia, es decir:
~~~ (x + y)^n = c_0 x^{n-0} y^0 + c_1 x^{n-1} y^1 + c_2 x^{n-2} y^2 + ... + c_{n-1} x^{n-(n-1)} y^{n-1} + c_n x^{n-n} y^0
~~~ (x + y)^n = c_0 x^n + c_1 x^{n-1} y + c_2 x^{n-2} y^2 + ... + c_{n-1} x y^{n-1} + c_n y^0
Los coeficientes c_i que aparecen en el desarrollo de las potencias binomiales son los que se extraen del triángulo de Tartaglia.
Vayamos a ejemplos concretos y con ello verificaremos la utilidad de esta construcción matemática.
~~~ n=0 ~~~ \longrightarrow ~~~ (x + y)^0 = 1
~~~ n=1 ~~~ \longrightarrow ~~~ (x + y)^1 = x^1 + y^1
~~~ n=2 ~~~ \longrightarrow ~~~ (x + y)^2 = x^2 + 2 x y + y^2
~~~ n=3 ~~~ \longrightarrow ~~~ (x + y)^3 = x^3 + 3 x^2 y + 3 x y^2 + y^3
~~~ n=4 ~~~ \longrightarrow ~~~ (x + y)^4 = x^4 + 4 x^3 y + 6 x^2 y^2 + 4 x y^3 + y^4
~~~ n=5 ~~~ \longrightarrow ~~~ (x + y)^5 = x^5 + 5 x^4 y + 10 x^3 y^2 + 10 x^2 y^3 + 5 x y^4 + y^5
~~~ n=6 ~~~ \longrightarrow ~~~ (x + y)^6 = x^6 + 6 x^5 y + 15 x^4 y^2 + 20 x^3 y^3 + 15 x^2 y^4 + 6 x y^5 + y^6
~~~ n=7 ~~~ \longrightarrow ~~~ (x + y)^7 = x^7 + 7 x^6 y + 21 x^5 y^2 + 35 x^4 y^3 + 35 x^3 y^4 + 21 x^2 y^5 + 7 x y^6 + y^7
~~~ n=8 ~~~ \longrightarrow ~~~ (x + y)^8 = x^8 + 8 x^7 y + 28 x^6 y^2 + 56 x^5 y^3 + 70 x^4 y^4 + 56 x^3 y^5 + 28 x^2 y^6 + 8 x y^7 + y^8
~~~ ..................................................
Este triángulo se utilizará también en combinatoria mediante la regla de Pascal, donde generaremos un triángulo tal que:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
\begin{pmatrix}
0 \\
0
\end{pmatrix}
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
\begin{pmatrix}
1 \\
0
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
1 \\
1
\end{pmatrix}
~~~~~~~~~~~~~~~~~~~~~~~~
\begin{pmatrix}
2 \\
0
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
2 \\
1
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
2 \\
2
\end{pmatrix}
~~~~~~~~~~~~~~~~
\begin{pmatrix}
3 \\
0
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
3 \\
1
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
3 \\
2
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
3 \\
3
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
4 \\
0
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
4 \\
1
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
4 \\
2
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
4 \\
3
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
4 \\
4
\end{pmatrix}
\begin{pmatrix}
5 \\
0
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
5 \\
1
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
5 \\
2
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
5 \\
3
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
5 \\
4
\end{pmatrix}
~~~~~~~~
\begin{pmatrix}
5 \\
5
\end{pmatrix}
..................................................................................
De forma que podríamos expresar:
~~~ (x + y)^n = \sum_{k=0}^n \binom{n}{k} x^{n-k} y^ksabiendo que:
~~~ \binom{n}{k} = \frac{n!}{k! (n-k)!}
~
~~~ n! = n~·~(n-1)~·~(n-2)~·~...~·~2~·~1
Veamos el desarrollo con un ejemplo con n=3:
~~~ n=3
~~~~~~~~~~~~~~~ (x + y)^3 = \binom{3}{0} x^3 + \binom{3}{1} x^2 y + \binom{3}{2} x y^2 + \binom{3}{3} y^3
~
~~~~~~~~~~~~~~~ (x + y)^3 = \frac{3!}{0! 3!} x^3 + \frac{3!}{1! 2!} x^2 y + \frac{3!}{2! 1!} x y^2 + \frac{3!}{3! 0!} y^3
~
~~~~~~~~~~~~~~~ (x + y)^3 = \frac{3~·~2~·~1}{1~·~3~·~2~·~1} x^3 + \frac{3~·~2~·~1}{1~·~2~·~1} x^2 y + \frac{3~·~2~·~1}{2~·~1~·~1} x y^2 + \frac{3~·~2~·~1}{3~·~2~·~1~·~1} y^3
~
~~~~~~~~~~~~~~~ (x + y)^3 = \frac{6}{6} x^3 + \frac{6}{2} x^2 y + \frac{6}{2} x y^2 + \frac{6}{6} y^3
~
~~~~~~~~~~~~~~~ (x + y)^3 = x^3 + 3 x^2 y + 3 x y^2 + y^3
Una de la propiedades más sorprendentes es la que relaciona este triángulo con la serie de Fibonacci y la proporción áurea, y sino observad los datos: