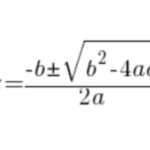Breve historia
Las matemáticas tienen joyas como este fantástico y maravilloso número tan emparentado con la naturaleza y los procesos naturales. El número áureo es el resultado de una de las sucesiones más fascinantes y famosas del mundo de las matemáticas, como es la serie de Fibonacci. Esta sucesión viene sugerida y debe su nombre al matemático italiano prerrenacentista, Leonardo Fibonacci o Leonardo de Pisa (1170-1240 d.c.), el cual la describió, así como otras grandes aportaciones como fueron la numeración arábiga, que a la postre tanto influiría en el desarrollo de la matemáticas en el mundo moderno, ya que introducía un tipo de numeración que incorporaba el cero y además facilitaba enormemente las operaciones matemáticas de multiplicación y división, tan complejas bajo la numeración romana. Pero volviendo a la sucesión de Fibonacci, esta es la que nos ocupa, y marca y determina un número conocido desde muy antiguo como el número de oro, número áureo o proporción áurea.
Descripción y desarrollo
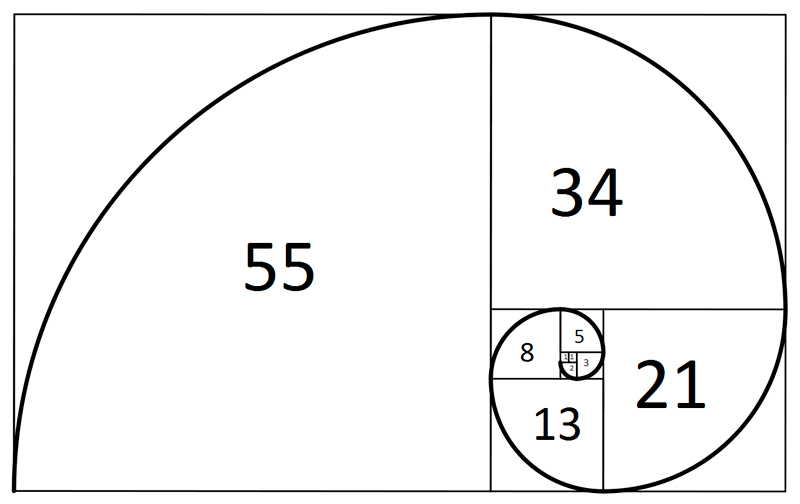
La sucesión es bien simple y se trata de números que se van formando tras la suma de los dos anteriores del modo en que se puede percibir aquí:
~~~ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55Se puede establecer entonces:
~~~ i \in \mathbb{N}~(1, 2, 3, 4, 5, ...)
~~~ S_{i} \in \mathbb{N}
~~~ S_{i = 1} = 0
~~~ S_{i = 2} = 1
~~~ S_{i > 2} = S_{i-2}~+~S_{i-1}
Como se puede ser observar fácilmente:
~~~ i=3 \Rightarrow S_{3-2} + S_{3-1} = S_{1} + S_{2} = 0 + 1 = 1
~~~ i=4 \Rightarrow S_{4-2} + S_{4-1} = S_{2} + S_{3} = 1 + 1 = 2
~~~ i=5 \Rightarrow S_{5-2} + S_{5-1} = S_{3} + S_{4} = 1 + 2 = 3
~~~ i=6 \Rightarrow S_{6-2} + S_{6-1} = S_{4} + S_{5} = 2 + 3 = 5
~~~ i=7 \Rightarrow S_{7-2} + S_{7-1} = S_{5} + S_{6} = 3 + 5 = 8
~~~ ...
Hasta ahora lo que hemos visto es la serie o sucesión de Fibonacci, pero ¿dónde está el número áureo o de oro? ¿de dónde surge? y ¿por qué es tan importante?
El número áureo, o la también llamada proporción áurea, es el resultado de la oscilación de la relación entre el número siguiente y el actual cuando está oscilación la llevamos al infinito, de modo que queda de la siguiente forma:
~~~ \varphi = lim_{x~\rightarrow~\infty}~\frac{S_{n+1}}{S_{n}} = 1,618033989...Se trata de un número irracional, que contiene infinitos números sin que estos repitan un patrón.
Podemos verificar de forma sencilla su oscilación y su tendencia en el infinito hacia el valor del número \varphi:
~~~ 2 / 1 = 2
~~~ 3 / 2 = 1.5
~~~ 5 / 3 = 1.66666...
~~~ 8 / 5 = 1.6
~~~ 13 / 8 = 1.625
~~~ 21 / 13 = 1.6154...
~~~ 34 / 21 = 1.619...
~~~ 55 / 34 = 1.6176...
~~~ ...
Como se puede observar, los valores son oscilantes por encima y por debajo del número \varphi
Esta relación es bastante peculiar ya que parece que cualquier sucesión numérica de orden 2 cuyos términos sean la suma de los dos anteriores derivan en el número áureo en su relación tendente al infinito entre el número siguiente y el actual.
La razón áurea al final es la relación que toman los segmentos de un rectángulo que cumplan:
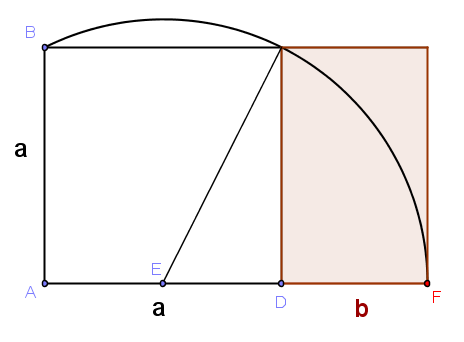
De la que se desprende que:
~~~ \varphi = \frac{a}{b}Y operando obtenemos:
~~~ \frac{a + b}{a} = 1 + \frac{1}{{a / b}} = \frac{a}{b}
~~~ 1 + \frac{1}{\varphi} = \varphi
Y despejando:
~~~ \varphi + 1 = \varphi^2De modo que llegamos a:
~~~ \varphi^2 - \varphi - 1 = 0Y resolviendo la ecuación de 2º grado llegamos a:
~~~ \varphi = \frac{1 + \sqrt{5}}{2} \approx 1,618033989...
Historias del número áureo
El número áureo es conocido desde antiguo, y ya en civilizaciones como el Antiguo Egipto, conocían este número, que aplicaron en sus construcciones como se puede observar en construcciones como las Pirámides de Gizá. Así como, los griegos clásicos también aplicaron el conocimiento de este número en su arquitectura como atestigua el Partenón.
Pero, ¿por qué razón resulta relevante este número? Pues sencillamente porque tiene una enorme aplicación a la geometría que presenta la naturaleza en la construcción de numerosas formas y seres vivos. Se trata del número estético por excelencia, de forma que las construcciones que presentan este número en sus proporciones son consideradas más armónicas en su estética, y así podemos observar obras arquitectónicas como el Partenón que presentan estas proporciones en sus medidas.
La espiral de Durero, que se construye tomando como base la secuencia de Fibonacci en su desarrollo, origen del número áureo, como ya hemos visto, inspira muchas geometrías espirales observadas en la naturaleza. Aquí podemos ver la construcción de esa espiral de Durero en base a la secuencia de Fibonacci.
Y observaremos como los Nautilus crean sus caparazones siguiendo la espiral:
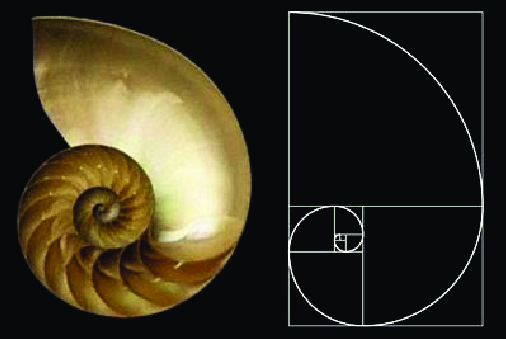
O el crecimiento de los girasoles siguiendo secuencias de Fibonacci y creando fractales:

O las galaxias con sus brazos en espiral inspirados en esa razón áurea y serie de Fibonacci: