Los logaritmos y sus operaciones

Los logaritmos son una de la herramientas matemáticas más importantes que es necesario conocer y dominar.

Pero ¿qué son los logaritmos? Pues básicamente es una operación inversa a la exponenciación, de modo que:

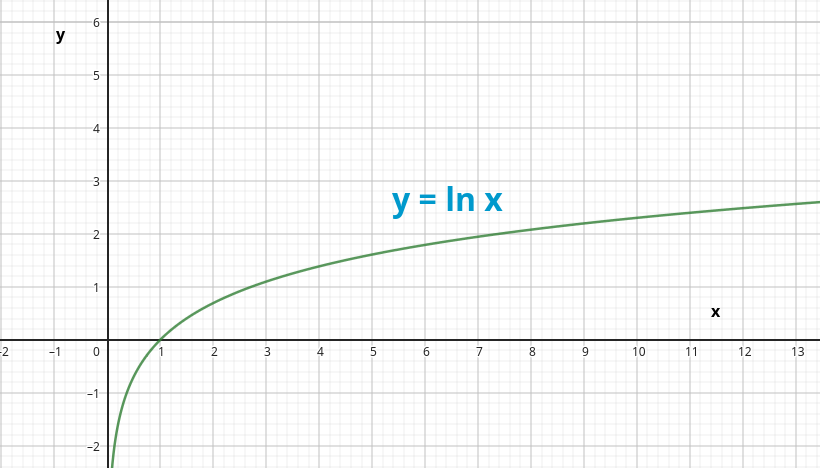
Si a = n^x , entonces:

~~~ log_{n}~a = x

Y ¿qué operaciones básicas podemos realizar con los logaritmos? Pues bien:

En primer lugar:

~~~ log_{n}~a^b = b~{log_{n}~a}

En segundo lugar:

~~~ log_{n}~{a~·~b} = {log_{n}~a}~+~{log_{n}~b}

y por tanto también se cumple que:

~~~ log_{n}~\frac{a}{b} = {log_{n}~a} - {log_{n}~b}

Vamos a poner ejemplos de esto utilizando como base logarítmica el número 10, ya que este nos va a permitir entender todo esto de una forma más intuitiva:

~~~ x = 10^3 = 1000

Si hacemos el logaritmo en base 10 de esa igualdad obtendremos:

~~~ log_{10}~x = log_{10}~10^3

Y si aplicamos las operaciones antes mencionadas:

~~~ log_{10}~x = 3~log_{10}~10

Como el logaritmo en base n de un número n es 1:

~~~ log_{10}~x = 3~·~1 = 3

Es decir, obtenemos que es 3, que es el exponente o el número de veces al que hay que elevar 10 para obtener x, y en efecto, obtenemos 1000 como esperábamos.

Ahora vamos a ver una operación como es el logaritmo de un producto o una división. Es importante notar que una división también se puede escribir como una operación de multiplicación, y por tanto aplicando lo que sabemos de los logaritmos terminaremos multiplicando por -1. Veámoslo:

Hemos dicho que:

~~~ log_{n}~a^b = b~{log_{n}~a}

y también:

~~~ log_{n}~(a~·~b) = {log_{n}~a} + {log_{n}~b}

Bien, pues entonces:

~~~ log_{n}~\frac{a}{b} = log_{n}~(a~·~b^{-1}) = {log_{n}~a} + {log_{n}~b^{-1}}
~~~ log_{n}~\frac{a}{b} = {log_{n}~a} + (-1)~·~{log_{n}~b} = {log_{n}~a} - {log_{n}~b}

Veamos esto con números:

~~~ log_{10}~(10^2~·~10^5) = {log_{10}~10^2} + {log_{10}~10^5}
~~~ log_{10}~(10^2~·~10^5) = 2~{log_{10}~10} + 5~{log_{10}~10} = 2 + 5 = 7

Y como:

~~~ log_{10}~(10^2~·~10^5) = log_{10}~{10^{2+5}} = log_{10}~{10^{7}} = 7~log_{10}~{10} = 7~·~1 = 7

Logaritmos frecuentes

Los logaritmos más frecuentes con los que se trabaja habitualmente en matemáticas son los que tienen como base el 10 o el número e, es decir, el número de Euler, número que está totalmente intrincado en el desarrollo de los procesos naturales, y por ello se le llama logaritmo natural o neperiano (por su descubridor John Napier).

Este último, el logaritmo neperiano tiene unas propiedades muy particulares, que hacen de él un referente en las matemáticas avanzadas, donde ya se empiezan a manejar las derivadas e integrales de funciones. Y ¿esto por qué es así? Pues vayamos a ello, porque merece la pena hacer una revisión de esto:

Sea f(x) una función de x:

~~~ f(x) = e^x

La derivada de esa función es una función que es igual si misma, y por tanto a la integral le ocurre exactamente lo mismo.

~~~ f\prime(x) = e^x

Y la integral genéricamente:

~~~ f(x) = e^x
~~~ \int{f(x)~dx} = \int{e^x~dx} = e^x

Las gráficas de representación de funciones logarítmicas suelen tener un aspecto como este (logaritmo en base 10):

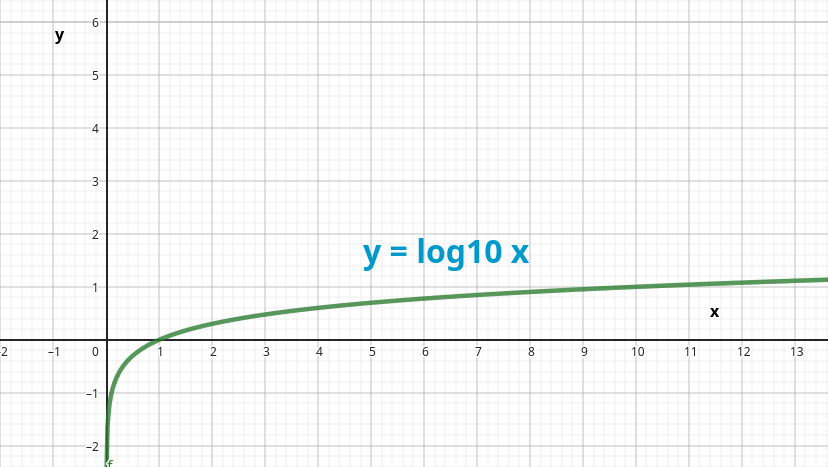
Para un logaritmo en base e: